IRR and APR for Programmers
Introduction
IRR (internal rate of return) is a finantial term often used when dealing with the stock market, pension funds, and other investments. Investment's IRR is a quick indication of how good (or bad) the investment is. Generally, the higher the IRR, the better you are doing. Positive IRR means you are earning money. Negative IRR means you are losing money.
APR is an IRR applied to loans, such as mortgages. APR is the rate of return the lender is earning. So, the higher the APR the more money your lender gets, and this means that generally you want a loan with the lowest APR (more about it later).
However, when you get into the details, things don't look that simple. The mathematics of the IRR is somewhat complicated. If your investment has irregular cash flow (sometimes up, sometimes down), there may be no IRR at all. Even more interestingly, there may be more than one value of the IRR. Shockingly, one of those values may be negative, and another positive, which would mean you are earning and losing money at the same time! Nevertheless, for the majority of investments IRR is a reasonably good indication of the investment quality.
Inflation and Deflation
The concept of the rate of return starts with a very simple reasoning. Paper money tend to lose value over time. This is called inflation. A thing that costs $100 today may cost $105 a year from now, i.e. its price would rise 5%. If prices of all goods rise 5% a year on average, we have 5% inflation.
Inflation can be arbitrary high, at least in theory. If prices double in a year it means 100% inflation. If prices triple, it's 200% inflaction. If prices rise 10 times, it is 900% inflation. In practice, when inflation is very high financial system breaks down, and people stop using the inflating money. They switch to something more stable: a different currency, a commodiy used as currency (gold, bottles of vodka, etc.), barter, or a combination thereof. But theoretically speaking inflation can be anything up to positive infinity.
Deflation is negative inflation, when prices drop. This is rare, but sometimes it does happen. If $100 item costs $95 a year from now it means 5% deflation, or negative 5% inflation. Deflation can never be higher than 100%. If the prices drop 2 times it's 50% deflation. If the prices drop 10 times, it's 90% deflation. If a year from now everything is handed out for free, it's 100% deflation. 110% deflation would mean that goods became cheaper than free, and this is not really possible.
Since deflation is negative inflation, we can state that inflation can range from -100% to positive infinity.
Discounted Future Payments
Discounting future payments means converting them to today's prices using expected inflation rate, also known as discount rate.
For example, if we expect 10% inflation, the prices would be multiplied by 1.1 in a year. So, $100 a year from now would buy us as much as $100/1.1 = $90.91 buys us today. In other words, under 10% inflation (discount) rate, $100 a year from now is roughly equivalent to $90.91 today. This is called a discounted value of a future payment. Discounts equally apply to the money we receive and the money we pay. Paying someone $100 a year from now would be roughly the same as paying them $90.91 today.
If we go forward two years, discounts deepen. If inflation is kept at 10%, the prices will rise 1.21 times in two years. Thus, $100 in to years equals only 100/1.21 = $82.64 in today's money.
Net Present Value
Net present value is a sum of all cashflow payments discounted for today. Naturally, it depends on the discount rate (inflation). Suppose we bought a bond for $100, then received $5 dividents for 3 years, then sold the bond for $101. Out cashflow then would be:
-100, 5, 5, 5, 101
where negative values mean we pay money and positive values mean we receive money. The net value of this investment is the sum of all payments, or $16. However, this is not the whole story, because net cashflow does not account for inflation.
Suppose we had 5% inflation. This means that the prices would rise 1.05 times each year, and the payments would be discounted by 1/1.05 = 0.9524 times each year. So, our net present value is now:
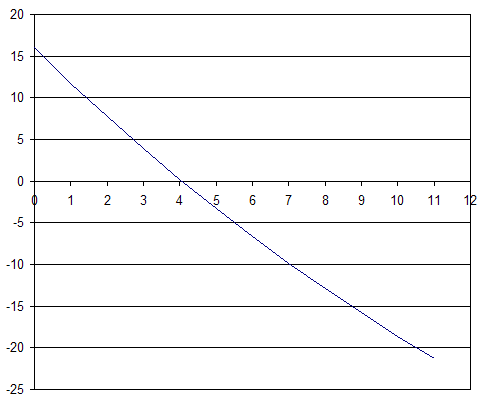
-100 + 5*0.9534 + 5*0.95242 + 5*0.95243 + 101*0.95244 = -3.29
This means that under 5% inflation our gain disappears and we actually end up losing money. Our investment performs worse than the 5% inflation rate. The net present value is a function of the cashflow itself and the discount (inflation) rate. In our particular case it looks like the graph below. Note that the NPV crosses zero at slightly over 4%.
Now, let's imagine a scenario similar to the previous one, but we could sell the bond only for $80 in the end. Our cashflow then would be like this:
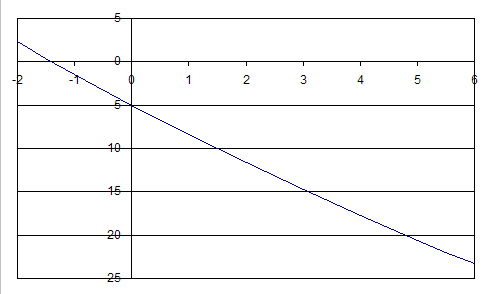
-100, 5, 5, 5, 80
Net value for this scenario is -5. The NPV graph for this scenario is below. We will need negative inflation to break even: the graph crosses zero at around -1.5%. This means we are losing money.
Internal Rate of Return
Internal rate of return for a cashflow is the discount rate at which the net present value is zero. For two examples above the IRR is approximately 4.1% and -1.5% respectively. In general, this means that in the first case we are earning money at the average rate of 4.1% per year, and in the second case we are losing money at the average rate of 1.5% per year.
However, things are not that simple. It is not guaranteed that for any arbitrary cashflow NPV will ever reach zero. Furthermore, if it does, it is not guaranteed that this will happen at only one point.
The simplest example of a case when NPV never reaches zero is when the money flows in only one direction. E.g. we paid $100 and then paid another $50. So, our cashflow is -100, -50. We never received aynthing back. No valid discount rate (above -100%) would reduce our loss to zero. Our initial loss of $100 is given and cannot be erased. The discount rate only influences our second loss ($50). Very high disconut rate will reduce it to zero, so NPV(+∞) = -100. Negative discount rate will make our $50 loss more significant, with NPV reaching negative infinity at the discount rate of -100%.
Another example of an irregular cashflow is
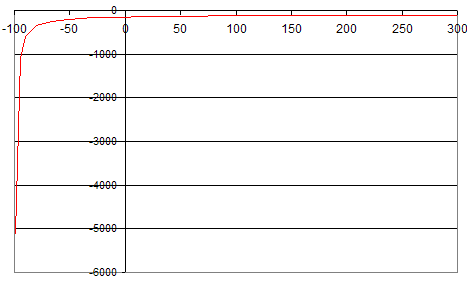
-10, 21.1, -11
NPV graph for this cashflow looks as follows:
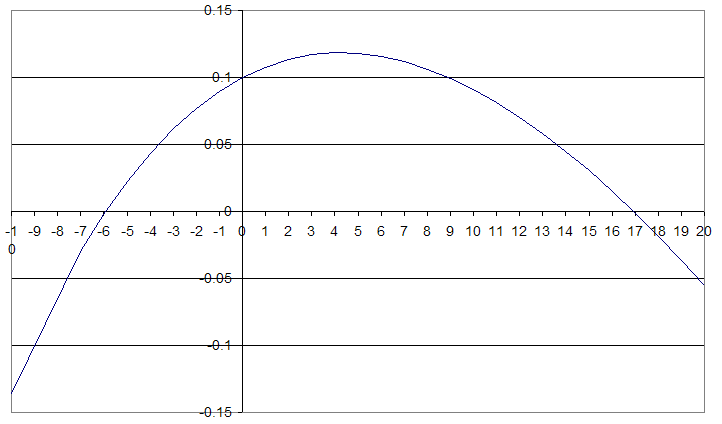
The graph crosses zero at two points: near -6% and near 17%. This means that we could claim that we are losing around 6% a year on average or that we are gaining around 17% a year at the same time!
This happens because the net value of our cashflow is almost zero, and the discount rate allows the second and the third payment to play against each other. With low discount rate the second payment gains the upper hand and overall NPV is positive. As discount rate increases, the importance of the second and third year decreases and at some point they fail to compensate for the initial loss of $10. At the discount rate of positive infinity our NPV would be exacly -10.
On the other hand, if we slide into the negative discount rate territory, this increases the importance of the last year loss. At some point it overtakes the second year gain and will drive NPV further and further down, approaching negative infinity as the discount rate approaches -100%.
This shows that the concept of IRR, although intuitively obvious, may sometimes lead to surprising results, where you gain and lose money at the same time.
Yearly, Monthly, and Daily Rates
In the discussion above we assumed that we receive or make payments yearly. IRR calculation can be equaly applied to any kind of periodic payments: monthly, weekly or even daily. However, in this case resulting IRR would be a monthly, weekly, or daily rate of return, and it must be converted to a yearly rate (annualized).
Monthly rates are typically converted to yearly rates by simply multiplying them by 12. Conversely, yearly rates are converted to monthly rates by diving them by 12. This is a common practice for all kinds of rates.
However, this calculation is not exact. It leads to an error in favor of the payment receiver. If rate x/12 is applied every month, total compounded interest for a year would be (1+x/12)12, which is greater than 1+x for any positive x.
For example if you have a "6%" mortgage this means monthly rate of 0.5%. Compounded yearly rate would be 1.00512 = 1.0617, or 6.17%. This is the real yearly rate you pay, not the quoted 6%. For a $300,000 mortgage this means overpaying about $500 a year.The higher the rate, the more significant the discrepancy. For "24%" mortgage at 2% a month the real yearly rate is 26.82%, or about $2500 overpay for $300,000 loan.
Things get even more confusing for daily rates. There are always 12 months in a year, but the number of days in a month and even the number of days in a year varies. There are multiple ways to attack this problem called day count conventions. E.g. the 30/360 convention assumes that each year has 360 days and each month has 30 days. This way interest between May 1st and June 15th would be the same as the one between February 1st and March 15th, notwithstanding the fact that the first interval is 45 calendar days and the second is only 42.
APR
Annual Percentage Rate (APR) is the lender's IRR for a mortgage. Morgtgage lenders came up with clever ways to increase their profit by introducing up front fees and points. Let's say you are offered a $300,000 loan at 5% yearly rate, but you need to pay a $1,000 origination fee and 2 points (2% of the loan amount, or $6,000) when signing the contract. Thus, you end up paying $7,000 to the lender for the privilege of getting the loan.
In practice this means that you receive only $293,000 upon signing the contract, but must make payments as if you received $300,000. So, the quoted 5% rate is not the whole story, the lender's real rate of return would be higher than that. APR was designed to expose such tactics and give consumers a more realistic idea of the expense of the mortgage. The lower the APR, the better for consumer. The lower the difference between the quoted interest rate and the APR, the less up front fees are involved. If there are no up front fees at all, APR would be equal to the mortgage interest rate.
For example: $300,000 loan, 5% rate, 5.05 APR means reasonable up front fees. $300,000 loan with 3% rate and 5.8% APR means huge up front fees and better be avoided. Calculating APR for floating rate mortages is somewhat tricky, since no one knows what the rate is going to be in the future. The APR is typically calculated using current market rates, and therefore is not very reliable, or sometimes downright misleading.
Mathematics of the IRR
NPV is a polynomial function of the depreciation ratio r related to the discount rate d as
r = 1/(1+d/100)
Conversely,
d = 100*(1/r-1)
NPV(r) = P0 + rP1 + r2P2 + ... + rnPn.
where P0...Pn are cashflow payments.
Valid range for d is between -100% and positive infinity. Valid range for r is between 0 (d=∞) and +∞ (d=-100). Negative values of r would mean that the money "change sign" every payment period. "Negative money" would mean that people give you money for the privilege of serving you with their goods. This might be nice, but it is a pure methematical fantasy that does not happen in real life.
The degree of the NPV polynomial equals to the number of payments minus one. If we have a 60 month loan, there will be 61 payments in the cashflow (getting the loan plus 60 loan payments), and thus the degree of the NPV polynomial will be 60. Every polynomial of an odd degree (e.g. r5 + 2r4+1) has at least one root. However, this root may lie in the area of negative r, and will not lead to a valid discout rate. So, a cashflow with even number of payments may still not have an IRR.
If the first payment and the last payment have different signs, the polynomial will have at least one positive root. Let's assume the fisrt payment is negative and the last payment is positive. When r=0 (d=+∞), NPV equals to the fisrt payment and is therefore negative. When r=+∞ (d=-100), NPV equals +∞. Since NPV is a continuous function, it must hit zero somewhere between r=0 and r=+∞ (intermediate value theorem). However, it is not guaranteed to be monotonic and may hit zero more than once.
If all payments but the first have the same sign, and the fisrt payment has the opposite sign, IRR value is guaranteed to exist and be unique. This is because NPV(r) would be a monotonic function in this case, and is guaranteed to hit zero exactly once between r=0 and r=+∞. Threfore, typical loans, bonds, etc. where initial purhase is followed by divident payments of the opposite sign, will always have a unique IRR. Irregular cashflows, however, may not have an IRR at all, or may have more than one IRR as we saw above.
Calculating the IRR
If the cashflow is known, IRR is a root of the equation NPV(r) = 0. Typically, this equation is solved by some numerical method, e.g. bianry search or secant method and is relatively straightforward. Things to watch out for are:
- There may be no IRR at all.
- The IRR may lie outside of your initial search limits.
- The IRR may be negative.
- There may be more than one value of the IRR.
- Secant method does not always converge.
